Omrekenen van eenheden
De informatie over het omrekenen bevat 6 onderdelen en wat gemengde opgaven.
Klik op een onderdeel om het te openen.
Weet je nog niet wat eenheden en grootheden zijn?
Lees dan de andere webpagina Grootheden & eenheden die daarover gaat.
Je gebruikt het omrekenen van eenheden meestal om:
- Een beter inzicht te krijgen in wat je hebt berekend.
10 cm³zegt je meer dan0,00001 m³. (toch staat hier twee keer dezelfde waarde!) - De juiste getallen in een formule in te vullen. Als je getallen in een formule invult, moeten alle eenheden van de getallen die je invult wel overeenkomen, anders gaat het mis.
Voorbeeld:
Een zwembad heeft een lengte van 25 meter, een breedte van 1500 centimeter en is 0,02 hectometer diep. Bereken hoeveel kubieke meter water er in het zwembad zit.
Je ziet dat er drie verschillende eenheden genoemd zijn. Je zult eerst deze drie getallen in dezelfde eenheid moeten zetten, alvorens je ze invult in de formule. Bovendien moet het eindantwoord ook nog eens in m³ zijn, dus alles moet worden omgerekend naar meters.
Het omrekenen naar meters:
l = 25 mb = 1500 cm = 15 mh = 0,02 hm = 2 mV = ?
|
|
V = l · b · hV = 25 · 15 · 2V = 750 cm³
|
Meer informatie over het oplossen van rekensommen met dit stappenplan (door mij ook wel 'Het Recept' genoemd) vind je op de webpagina Recept.
Je hebt veel verschillende soorten eenheden:
- Eenheden van afstand zijn bijvoorbeeld: kilometer (km), meter (m), centimeter (cm)
- Eenheden van snelheid zijn bijvoorbeeld: meter per seconde (m/s), kilometer per uur (km/h)
- Eenheden van Volume zijn bijvoorbeeld: kubieke meter (m³), kubieke centimeter (cm³), liter (l), centiliter (cl)
- Eenheiden van Temperatuur: graden Celsius (°C), Kelvin (K), graden Fahrenheit (°F)
Voor elke grootheid bestaan vaak meerdere eenheden. Je zult dus regelmatig eenheden moeten omrekenen.
Voorbeeld:
1 kilometer = 1000 meter
Bij het werken met eenheden gebruik je onderstaande voorvoegsels:
Wetensch. notatie = Wetenschappelijke notatie.
Dat zijn er heel wat (er zijn er nog meer !). Zorg dat je in elk geval de voorvoegsels van Mega tot micro goed kent. Ze zijn blauw gemarkeerd.
Zet je deze in een rij van links naar rechts, dan krijg je (nog even zonder Mega en micro):
| kilo (k) |
hecto (h) |
deca (da) |
--- |
deci (d) |
centi (c) |
milli (m) |
(Bij de --- staat altijd de eenheid zelf, die geen voorvoegsel heeft)
Dit is wat we vanaf nu 'het rijtje' noemen. Leer dit rijtje uit je hoofd!
We nemen als voorbeeld de grootheden Afstand, Volume en Energie, en zetten de voorvoegsels voor de eenheid. Dan krijg je dus per grootheid een hele reeks van eenheden:
De grijze cellen zijn eenheden die je niet vaak gebruikt. Toch moet je de voorvoegsels kennen: ze vormen onderdeel van het rijtje en het rijtje heb je nodig als je gaat omrekenen. Leer het rijtje met voorvoegsels van Mega tot micro uit je hoofd, dan kun je iedere eenheid 'maken'.
4.1 Omrekenen van afstanden
Voor het omrekenen gebruik je dus het zogenaamde rijtje. Neem als voorbeeld steeds het rijtje eenheden voor afstand, maar het onderstaande verhaal geldt ook voor andere eenheden.
Het rijtje voor afstanden:
| kilometer (km) |
hectometer (hm) |
decameter (dam) |
meter (m) |
decimeter (dm) |
centimeter (cm) |
millimeter (mm) |
De regels:
- 1 stap naar links in het rijtje = komma 1 naar links in het getal
- 1 stap naar rechts in het rijtje = komma 1 naar rechts in het getal
Voorbeeld 1:
3,5 km is hoeveel meter?
In je rijtje zie je dat om van km naar m te gaan, je 3 stappen naar rechts moet gaan.

3 stappen naar rechts, dus komma 3 plaatsen naar rechts: 3,5 km = 3500 m
Zie je dat er maar twee nullen bijgekomen zijn? Werk dus NOOIT met'nullen erbij' of 'nullen eraf', maar verplaats de komma! Want anders gaat het mis.
Voorbeeld 2:
Je wilt weten hoeveel decimeter 4,02 millimeter is. Je weet dus het aantal millimeter en moet omrekenen naar decimeters.
Dan moet je in het rijtje 2 stappen naar links (controleer dat!), dus de komma gaat in het getal 4,02 twee plaatsen naar links:
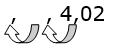
2 stappen naar links, dus komma 2 plaatsen naar links:
4,02 mm = 0,0402 dm
Video-uitleg over hoe je werkt met het rijtje met voorvoegsels:
Oefenopgaven
| 1. | 10 km | = | m |
| 2. | 1,4 hm | = | m |
| 3. | 0,1 dam | = | mm |
| 4. | 10 cm | = | m |
| 5. | 1000 cm | = | hm |
| 6. | 2,5 km | = | cm |
| 7. | 2560,8 cm | = | km |
| 8. | 4567 mm | = | m |
| 9. | 0,00345 km | = | m |
| 10. | 0,00345 hm | = | mm |
4.2 Omrekenen van volumes
Voor volume geldt precies dezelfde regel als bij afstand. Ook hier gebruik je het rijtje met voorvoegsels. Voor vloeistoffen en gassen gebruik je meestal de liter als eenheid (hoewel het net zo goed de m³ kan zijn)
Het rijtje voor volumes is dan:
| kiloliter (kl) |
hectoliter (hl) |
decaliter (dal) |
liter (l) |
deciliter (dl) |
centiliter (cl) |
milliliter (ml) |
Voorbeeldopgaven
Controleer met het rijtje de antwoorden.
| - | 1 kl | = | 1000 l |
| - | 1 dl | = | 10 cl |
| - | 100,54 cl | = | 10,054 dl |
| - | 1000 ml | = | 10 dl |
Voor het volume worden ook andere eenheden gebruikt. Bij vaste stoffen gebruik je meestal als eenheid de kubieke meter.
Het rijtje ziet er dan zo uit:
| kubieke kilometer (km³) |
kubieke hectometer (hm³) |
kubieke decameter (dam³) |
kubieke meter (m³) |
kubieke decimeter (dm³) |
kubieke centimeter (cm³) |
kubieke millimeter (mm³) |
Dat drietje rechtsboven is een macht van 3 en spreek je uit als 'kubieke' en je spreekt die als eerste uit. Dus 'kubieke meter' en niet 'meter kubieke'.
Dat drietje krijg je omdat je 3 keer een afstand met elkaar vermenigvuldigt om het volume te krijgen: V = l x b x h
Het resultaat is dus 'afstand tot de macht 3'
Dat drietje zorgt er helaas er ook voor dat het trucje met de komma schuiven niet zomaar meer werkt. Volgens de truc zou 1 m³ gelijk zijn aan 10 dm³ (komma 1 naar rechts)
Maar dat is niet waar: 1 m³ = 1000 dm³ De komma moet dus 3 naar rechts in plaats van 1 naar rechts!
Conclusie: Het getalletje rechtsboven de eenheid is gelijk aan het aantal plaatsen dat de komma naar links/rechts moet bij elke stap in het rijtje. Elke stap telt voor drie!
Voorbeeld 1:
0,5 dm³ = cm³ ?
Van dm³ naar cm³ is 1 stap naar rechts in je rijtje, maar vanwege het drietje telt elke stap nu voor 3!
Dus de komma gaat 3 naar rechts:
0,5 dm³ = 500 cm³
Voorbeeld 2:
3545,8 dm³ = m³ ?
1 stap naar links in je rijtje, maar de komma dus 3 stappen naar links schuiven:
3545,8 dm³ = 3,5458 m³
Voorbeeld 3:
0,000345 km³ = m³ ?
3 stappen naar rechts in je rijtje, maar de komma dus 3 x 3 = 9 stappen naar rechts schuiven:
0,000345 km³ = 345000 m³
Oefenopgaven
| 11. | 3,5 m³ | = | dm³ |
| 12. | 0,46 dm³ | = | cm³ |
| 13. | 0,5 m³ | = | dm³ |
| 14. | 5000 dm³ | = | m³ |
| 15. | 500.000 cm³ | = | m³ |
EXTRA OPDRACHT:
Neem 5 plankjes hout en maak er een kubus van met een opening aan de bovenkant en met als binnenafmetingen: 10 cm.
Dus 10 cm diep, 10 cm breed en 10 cm lang
Lijm de stukken aan elkaar met watervaste lijm en laat goed drogen.
Pak een literfles en vul deze met water. Niet helemaal tot aan de rand maar net zover als de fles normaal met drank gevuld is. Een maatbeker met precies 1 liter water is nog beter natuurlijk.
Giet de literfles/maatbeker leeg in je zelfgemaakte kubus. Past het er in???
4.3 Liters naar kubieke meters omrekenen
Als je de extra opdracht van de vorige paragraaf hebt uitgevoerd, zul je hebben gemerkt dat er precies 1 liter water in de kubus gaat. Met de formule V = l·b·h kun je het volume van de kubus ook berekenen:
l = 10 cmb = 10 cmh = 10 cmV = ?
|
|
V = l · b · hV = 10 · 10 · 10V = 1000 cm³
|
Je kunt dus nu zeggen dat 1000 cm³ = 1 liter
Met omrekenen kun je berekenen dat 1000 cm³ = 1 dm³ (ga dit na met je rijtje!)

Ofwel:
1 liter = 1 dm³
En dat betekent ook:
1000 liter = 1 m³
Leer in elk geval de eerste uit je hoofd! Daarmee kun je nu twee verschillende eenheden van Volume in elkaar omrekenen.
Pas wel op dat als je het rijtje van liters gebruikt, de komma maar 1 plaats verspringt per stap, en als je het rijtje van kubieke meters gebruikt, de komma 3 plaatsen verschuift per stap.
Als je wilt omrekenen van de ene eenheid van volume naar de andere eenheid, kun je het beste eerst omrekenen naar liters of dm³.
Voorbeeld 1:
100 cm³ = cl
Eerst cm³ omrekenen naar dm³. Kijk in het rijtje: dat is 1 stap naar links en dus de komma 3 naar links verplaatsen: 100 cm³ = 0,1 dm³
En 0,1 dm³ = 0,1 liter, want je leerde zojuist: 1 liter = 1 dm³
Nu nog 0,1 l omrekenen naar cl. Dat is de komma 2 naar rechts verplaatsen: 0,1 l = 10 cl
Het antwoord is dus: 10 cl
Voorbeeld 2:
4 hl = m³
Eerst omrekenen naar liters, want dan kun je 1 liter = 1 dm³ gebruiken. Dat is de komma 2 naar rechts verplaatsen: 4 hl = 400 l en dus: 400 l = 400 dm³
Nu nog 400 dm³ omrekenen naar m³. Dat is de komma 3 naar links verplaatsen: 400 dm³ = 0,4 m³
Het antwoord is dus: 0,4 m³
Video-uitleg over omreken van Volume ('liters'):
Oefenopgaven
| 16. | 1 dm³ | = | l |
| 17. | 1000 l | = | m³ |
| 18. | 456 cm³ | = | l |
| 19. | 123,456 cm³ | = | dl |
| 20. | 50.000 cl | = | m³ |
4.4 Omrekenen met oppervlakken
Bij het berekenen van Volumes vermenigvuldig je 3 keer een afstand met elkaar: lengte x breedte x hoogte. Je krijgt dan bij de eenheid een 3 rechtsboven.
Voorbeeld: m³ of dm³
Bij het berekenen van oppervlakten vermenigvuldig je 2 afstanden met elkaar: lengte x breedte.
Je krijgt dan bij de eenheid een 2 rechtsboven.
Voorbeeld: m² of cm²;
Dit betekent dat je in het rijtje bij elke stap de komma 2 naar links/rechts moet verschuiven.
Elke stap telt voor twee!
Voorbeeld-1:
Een rechthoek heeft een lengte van 7,5 cm en een breedte van 9 cm
De oppervlakte is dan:
l = 7,5 cmb = 9 cmA = ?
|
|
A = l · bA = 7,5 · 9A = 67,5 cm²
|
67,5 cm²= m²
Van cm naar m is 2 stappen naar links in het rijtje. Maar elke stap telt nu voor 2, dus 4 stappen naar links met de komma.
67,5 cm² = 0,00675 m²
Voorbeeld-2:
45000 mm²= m²
Van mm naar m is 3 stappen naar links maar elke stap telt voor 2, dus 6 stappen naar links met de komma:
45000 mm² = 0,045 m²
Oefenopgaven
| 21. | 1 m² | = | dm² |
| 22. | 0,45 m² | = | cm² |
| 23. | 500 mm² | = | dm² |
| 24. | 60,5 dm² | = | m² |
| 25. | 4000 dm² | = | dam² |
De truc met de komma schuiven werkt alleen in het rijtje van kilometer tot en met millimeter. Zoals je in de grote tabel op deze pagina kunt zien, gaat het daarbuiten met stappen van 3. Als je dus van kiloJoule wilt omrekenen naar MegaJoule, zul je dus 3 stappen moeten schuiven met de komma, terwijl ze toch naast elkaar in het rijtje staan. Sommige machten van 10 hebben gewoon geen voorvoegsel gekregen...
Voorbeeld:
2000 kJ = 2 MJ6 MJ = 6000 kJOefenopgaven
| 26. | 3,5 MJ | = | kJ |
| 27. | 0,3 MJ | = | J |
| 28. | 0,3 GL | = | MJ |
| 29. | 3,5 µJ | = | mJ |
| 30. | 0,3 TJ | = | MJ |
Voor de toetsen in klas 2 en 3 hoef je als leerling bij mij (!) alleen de voorvoegsels Mega tot en met micro uit de tabel te kennen. Vraag je eigen docent welke voorvoegsels jij moet kennen.
Als de eenheid in een breuk in de noemer staat (bijvoorbeeld bij snelheid in km/h of m/s), dan moet je oppassen.
Je hebt bij breuken al geleerd dat als je de noemer bijvoorbeeld 2 keer zo klein maakt, de breuk zelf 2 keer zo groot wordt.
Kijk maar:
→
En 1 is 2 x zo groot als 0,5
Je voelt nu hopenlijk al aankomen dat als de eenheid die je wilt omrekenen in de noemer van een breuk staat, de de komma dus precies de andere kant op moet bewegen!
Voorbeeld
Voorwerpen hebben een bepaalde 'dichtheid'. De dichtheid ρ van een voorwerp zegt iets over hoe dicht de moleculen in die stof op elkaar zitten. De dichtheid bereken je met ρ = m/V (massa gedeeld door volume).
Als eenheden van dichtheid kun je dus krijgen: g/cm³ of g/dm³ of kg/dm³ of kg/³ of ...
Dit zijn dus voorbeelden van eenheden die uit een breuk bestaan.
Voorbeeld-1
Wil je dus bijvoorbeeld 5 g/cm³ omrekenen naar g/dm³, dan moet je opletten: de komma moet de andere kant op dan normaal.
In het normale rijtje moet je 1 stap naar links om van cm naar dm te gaan, en vanwege het 3-tje geldt elke stap dus voor 3, dus 3 naar links.
Maar omdat de eenheid die je wilt omrekenen in de noemer staat, moet de komma dus 3 naar rechts.
Dus: 5 g/cm³ = 5000 g/dm³
Voorbeeld-2
300 kg/dm³ = kg/cm³
Van dm³ naar cm³ is 1 plaats naar rechts in je rijtje en elke stap telt voor 3, dus 3 naar rechts. Maar omdat de eenheid in de noemer staat, moet de komma dus juist 3 naar links:
300 kg/dm³ = 0,3 kg/cm³
Voorbeeld-3
300 kg/dm³ = g/cm³
Je ziet dat zowel de eenheid in de teller, als die in de noemer moet worden omgerekend. We beginnen met de teller, daar werkt het rijtje 'normaal'.
300 kg = 300.000 g (Komma 3 naar rechts in je rijtje)
... dus 300 kg/dm³ = 300.000 g/dm³ (dit is een tussenstap)
Nu de noemer: van dm³ naar cm³ is 1 plaats naar rechts in je rijtje en elke stap telt voor 3, dus 3 naar rechts. Maar omdat de eenheid in de noemer staat, moet de komma dus juist 3 naar links:
300 kg/dm³ = 300 g/cm³
Je had ook eerst de noemer mogen omrekenen en daarna de teller, maakt niet uit.
Oefenopgaven
| 31. | 54 g/cm³ | = | g/dm³ |
| 32. | 54 g/cm³ | = | kg/cm³ |
| 33. | 54 g/cm³ | = | kg/dm³ |
| 34. | 54 g/cm³ | = | g/mm³ |
| 35. | 54 g/cm³ | = | kg/m³ |
| 36. | 32,3 km | = | dam |
| 37. | 323,6 cm | = | km |
| 38. | 58,6 g | = | mg |
| 39. | 88,76 dm | = | hm |
| 40. | 48 g/cm³ | = | g/dm³ |
| 41. | 5 m³ | = | kl |
| 42. | 0,04 dm² | = | mm² |
Antwoorden
36. 3230 dam
37. 0,003236 km
38. 58600 mg
39. 0,08876 hm
40. 48000 g/dm³
41. 5 kl
42. 400 mm²
| 43. | 0,012 kg | = | mg |
| 44. | 200 cl | = | dl |
| 45. | 0,012 km | = | mm |
| 46. | 200 cm | = | dm |
| 47. | 4000 cm² | = | m² |
| 48. | 844 dm² | = | m² |
| 49. | 456 dam | = | hm |
| 50. | 4567 cm³ | = | mm³ |
| 51. | 4567 cm³ | = | dm³ |
| 52. | 4 kg/dm³ | = | g/cm³ |
| 53. | 800 kg/dm³ | = | kg/cm³ |
| 54. | 3 g/cm³ | = | kg/m³ |
| 55. | 24 l | = | dm³ |
| 56. | 24 l | = | ml |
| 57. | 100 kl | = | m³ |
Wil je de antwoorden van de opgaven ontvangen? Ga naar het contactformulier en lees daar wat je moet doen. (Als je les van mij hebt, gebruik dan NIET het formulier maar vraag het me gewoon...)
De content op deze website is auteursrechtelijk beschermd. Niets van deze website mag worden gekopieerd of verwerkt onder welke vorm dan ook zonder voorafgaandelijke schriftelijke toestemming van de auteur.